Prédire l'incertain. Au poker et dans la vie

• 25 juin 2014
• petiteglise
• 7373
•  PA  1
• 49 Commentaires

Dans l’article "Les joueurs de poker sont plus intelligents que la moyenne", nous avons découvert l’Intelligence Prédictive : la capacité à prédire l’incertain et à agir en accord avec ces probabilités. Dans cet article, je vous propose d’améliorer votre capacité à prédire l’incertain.

Les joueurs de poker sont plus intelligents que la moyenne.

Comprendre le théorème de Bayes

Vous estimez la probabilité d’un événement. Vous voyez ensuite un indice se produire. Comment allez vous changer la probabilité initiale de l’évènement ?
Il existe un théorème pour cela, créé par Thomas Bayes il y a quelques 250 ans.

Je vous propose une mise en situation qui va servir de base pour la compréhension du théorème.

Vous jouez régulièrement en HU contre un fish et gagnez 60% du temps. Il vous invite à jouer chez lui. Vous êtes un peu méfiant et vous dites qu’il y a 10% de risque qu’il triche. Devez-vous accepter ?

On va considérer que s’il triche, vous n’avez aucune chance de gagner.
Votre taux de succès est donc de : 0.9 * 0.6 = 0.54
Autrement dit, sur les 90% de chances qu’il ne triche pas, vous allez gagner 60% du temps soit 54% en tout. Il est donc intéressant de jouer.

Vous jouez donc, mais vous perdez le premier HU. Il vous propose une revanche, acceptez-vous ?

Un raisonnement trop hâtif serait de se dire qu’il faut accepter car on a 54% de chance de gagner. En effet, la probabilité qu’il triche a augmenté.

Pas convaincu ? Alors imaginez que vous acceptiez la revanche et perdez à nouveau. Puis encore le 3ème match et le 4ème et ainsi de suite… Si vous perdez 10 matchs de suite contre un joueur moins fort, vous serez d’accord que la probabilité qu’il triche n’est plus de 10% mais bien au delà. A chaque nouveau match perdu, la probabilité que votre adversaire soit un tricheur augmente, et ce dès le premier match perdu.

Mais la question est : quelle est la probabilité qu’il triche, sachant que vous avez perdu le premier match ?

Intuitivement, ce n’est pas simple à estimer.
Elle était de 10% et a augmenté. Est-ce 11% ? 15% ? 20% ? 30% ?

Grâce au théorème de Bayes, on peut donner la probabilité exacte.

Pour expliquer d’où vient la formule, je vais reprendre quelques notions de proba.

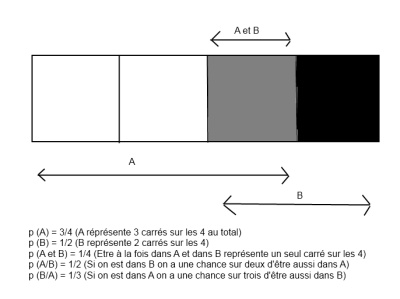Soient A et B deux événements.
La probabilité que A et B arrivent est :
p (A et B) = p (A) * p(B/A)
où p (B/A) signifie la probabilité de B sachant A

Attention, de manière générale, la probabilité p (A et B) n’est PAS égale à p(A)*p(B).

Exemple : La probabilité que notre première hole card soit un As est de 4/52, appelons cette probabilité p(A).
Et la probabilité que notre deuxième hole card soit un As est identique (on a ni plus ni moins souvent un As en carte de gauche qu’en carte de droite. Appelons cette probabilité p(B).
On a p(A) = p(B) = 4/52
La probabilité d’avoir deux As n’est PAS 4/52*4/52 mais est : p(A et B) = p(A) * p(B/A) où p(B/A) est la probabilité d’avoir un as en deuxième carte sachant que notre première carte est déjà un As : 3/51
p (A et B) = 4/52*3/51= 0.0045=0.45%

On a donc bien p(A et B) = p(A) * p(B/A)
On a donc aussi p(A et B) = p(B) * p(A/B)
Et donc p(A) * p(B/A) = p(B) * p(A/B)
En divisant par p (B) on obtient le fameux théorème de Bayes :
p (A/B) = p (A) * p (B/A) / p (B)

Si on appelle l’hypothèse H et l’indice I, on a :
p (H/I) = p (H) * p(I/H) / p (I)
Soit en français : la probabilité d’une hypothèse sachant un indice est égale à la probabilité a priori de l’hypothèse fois la probabilité de l’indice sachant l’hypothèse, divisée par la probabilité a priori de l’indice.

Dans notre exemple, l’hypothèse est qu’il triche et l’indice qu’on a perdu le premier match.
p (H) = 0.1 (la probabilité qu’il triche était a priori de 10%)
p (I/H) = 1 (la probabilité qu’il gagne sachant qu’il triche est de 100%=1)
p (I) = 0.46 (la probabilité que l’on perde ce premier match était a priori de 46%)
Et donc : p (H/I) = 0.1*1/0.46 = 0.22
Sachant que l’on a perdu le premier HU, la probabilité qu’il triche est maintenant de 22% !

La probabilité de gagner est donc de 0.78*0.6 = 0.47
Il faut donc refuser la revanche… Même si vous ne pouvez pas décemment accuser votre adversaire de triche (moins d’une chance sur quatre) vous n’avez plus la cote pour jouer.

L’intuition bayesienne

Prenons l’exemple du poker, qui est un parfait jeu bayésien. En effet, avant que vous ne receviez vos cartes, le range de chaque adversaire est constitué de 1326 combinaisons possibles et équiprobables. A chaque nouvel indice (nouvelle street ou move adverse) on réajuste les probabilités de ces combinaisons selon un raisonnement bayésien. C’est exactement le principe du range adverse.

Par exemple, quand un joueur 3-bet préflop, il y a beaucoup d’As dans son range (autrement dit, la probabilité des combinaisons avec As augmente). Mais si on voit deux As au flop, il y en aura beaucoup moins (autrement dit, la probabilité des combinaisons avec As diminue).

Les tout débutants au poker ne raisonnent même pas en terme de range. Ensuite, quand on commence à découvrir le concept, évaluer les changements de range à chaque indice est souvent un processus conscient et trop long pour être appliqué correctement en temps réel. Ces joueurs intermédiaires doivent donc se rabattre sur leur intuition, rarement correcte. Seuls les bons joueurs ont une bonne intuition pokero-bayésienne et peuvent évaluer très rapidement les ranges adverses avec une précision et une rapidité remarquable, sans effort, en tous cas pour les spots qu’ils ont vus et revus.

Il en va de même dans la vie de tous les jours, où l’on ne peut pas sortir un papier, poser et résoudre une équation avant d’évaluer une probabilité. Nous devons nous fier à notre intuition. Or celle-ci est sujette à de nombreux biais, qu’il est donc nécessaire de comprendre.

Le biais de représentativité

Madame X est intelligente, calculatrice, autoritaire et toujours habillée avec classe.
A votre avis, le plus probable est que Madame X soit :
PDG d’une entreprise dans le luxe
PDG d’une entreprise d’un autre domaine
Enseignante

La description de Madame X correspond au cliché qu’on peut avoir des PDG dans le luxe. C’est pourtant la réponse la moins probable. Le plus probable étant qu’elle soit enseignante. En effet, il y a tellement plus d’enseignantes que de PDG dans la population générale, que parmi toutes les femmes “intelligentes, calculatrices, autoritaires et toujours habillées avec classe”, il y a plus d’enseignantes que de PDG.

Ce n’est pas parce qu’un élément est représentatif d’une population, qu’il est probable qu’il appartienne à cette population.

L’ignorance du taux de base

C’est un biais proche de celui de représentativité.

Rappelez-vous l’énigme que je vous avez posée dans l’article précédent : L’arganie est une maladie qui touche 1 personne sur 10 000. Il existe un test fiable à 99%. Votre test est malheureusement positif, quelle est la probabilité que vous soyez malade ?

La mauvais réponse typique est de dire 99%. Ce qui ne prend pas en compte le taux de base. On peut utiliser Bayes pour obtenir la réponse précise (environ 0,98%).

Mais intuitivement, on peut simplement se dire qu’on part d’un événement très rarement vrai et qu’il se passe quelque chose de juste fréquemment vrai. Ce quelque chose de fréquent transforme le très rare en rare. Mais certainement pas en quelque chose de très probable.

Un exemple typique de poker : Vous avez KK et un adversaire vous 5-bet all-in préflop. Sans autre information, il vous faut évidemment payer. Tout au début, la probabilité qu’il ait AA est très rare (de 0,45%), elle augmente d’un poil quand vous recevez KK, puis grandement quand il 3-bet et encore plus quand il 5-bet, mais le plus probable est que vous ayez encore la cote pour payer.

La régression vers la moyenne

Avec l’équipe de France de foot, c’est simple : quand elle est critiquée, elle brille et quand elle encensée, elle déçoit. Beaucoup ont remarqué cette bizarrerie et y vont de leur explication : “les joueurs sont des enfants gâtés, faut les engueuler pour qu’ils se bougent” ou “les journalistes ne comprennent rien au ballon rond”.

Il y a aussi, voire surtout, une simple explication statistique : la victoire au foot dépend de la qualité de l’équipe mais aussi d’un énorme facteur chance (arbitrage, forme, blessures, poteaux sortants/rentrants, faux rebonds, etc). Quand les français brillent, c’est en partie dû à la chance. Quand elle tourne, ce qui est inéluctable, ils déçoivent en comparaison. Et quand ils jouent vraiment mal, c’est en partie dû à la malchance, qui elle aussi finit par tourner.

L’équipe de France a un niveau moyen (en gros 8ème nation mondiale si on se réfère au classement Elo, a priori bien meilleur que le classement FIFA). Elle joue parfois bien mieux, parfois bien plus mal, mais après une période exceptionnelle, elle se rapprochera de ce niveau moyen.

Ce phénomène s’appelle la régression vers la moyenne et existe dans bien des domaines. Pour en revenir au foot, cet article étant écrit en pleine coupe du monde après deux excellents matchs de l’équipe de France, si en cas d’élimination vous entendez un “ils se sont relâchés / trop de confiance en eux après leur début / ils ont pris leur adversaire de haut” vous pourrez répondre “simple régression vers la moyenne”.

La “malédiction de Sports illustrated”  (le plus grand hebdo sportif aux USA) veut que le sportif ou l’équipe qui fait la couverture ait moins de succès après la parution. Vous aurez compris qu’il n’y a rien de maléfique là dedans…

La taille de l’échantillon

Nombre de joueurs s’étant essayés au poker en ligne le temps de quelques parties arrêtent car ils pensent que c’est rigged. “J’ai perdu tous mes coins flips” “J’ai eu trois fois AA tapis préflop et à chaque fois perdu”.
En revanche, la très grande majorité des regs pensent que la distribution est aléatoire.
Bien sûr on peut penser que les fishs perdent car ils jouent mal et sont de mauvaise foi, mais dans le lot il y en a qui ne mentent pas.

L’explication est là encore statistique : plus un échantillon est faible, plus il a de chances de ne pas être représentatifplus un échantillon est faible, plus il a de chances de ne pas être représentatif. Sur très peu de mains, il est normal que certains aient beaucoup de (mal)chance.

Le biais de disponibilité

En Français, à votre avis, il y a t-il plus de mots commençant par S ou de mots avec un S en troisième position ?

A part si vous vous dites (avec raison !) qu’il y a un piège, vous allez chercher des mots qui commencent par un S, vous allez en trouver facilement puis chercher des mots avec un S en troisième place, en trouvez que difficilement et conclure qu’il y a plus de mots qui commencent par S. Ce qui est faux.

Cela montre le biais de disponibilité : plus il est facile de se souvenir d'un événement, plus on a tendance à le considérer comme fréquent.plus il est facile de se souvenir d’un événement, plus on a tendance à le considérer comme fréquent.

Cette facilité de souvenir induisant en erreur peut être due à divers facteurs, comme par exemple le traitement médiatique (on surestime la probabilité de mourir assassiné mais on sous-estime la probabilité de mourir d’une chute chez soi pourtant 20 fois plus grande)

Mécompréhension de l’indépendance des probabilités

Une des erreurs typiques déjà vue est de ne pas tenir compte de la dépendance des événements. Par exemple, dans le cas des faux positifs. La probabilité que le test soit correct dépend de la prévalence de la maladie dans la population. Mais on constate parfois l’effet inverse : inventer une dépendance entre des événements indépendants !

Exemple : je lance une pièce 4 fois de suite, est-il plus probable d’obtenir (dans l’ordre)
pile-face-pile-face
ou pile-pile-pile-pile ?

Ces deux séries ont la même probabilité. La résultat d’un lancer de pièce est indépendant du lancer précédent. En effet, le hasard n'a pas de mémoire. A chaque fois, la proba de pile est la même que celle de face est vaut ½. La proba de chacune de ces séries est donc de 1/16.

Le hasard n'a pas de mémoire !

Let’s make a deal était un jeu télévisé que l’on peut résumer ainsi : Le candidat doit choisir une porte parmi trois. Deux portes sont vides, l’une contient un prix. Après le choix du candidat, le présentateur ouvre une porte qu’il sait vide. Il demande ensuite au candidat s’il veut garder son premier choix ou changer de porte.

La très grande majorité raisonne : la proba d’avoir bon était 1/3, maintenant, sachant qu’il a ouvert une porte vide, elle est de 1/2. Ce qui est totalement faux. La proba initiale est bien de 1/3, mais comme le présentateur peut et va toujours ouvrir une porte vide, qu’il le fasse ne nous apprend rien et ne change rien à cette proba.

Une fois la porte ouverte, la probabilité que notre choix initial soit correct est donc de 1/3 et la proba qu’il soit faux de 2/3. Et comme, “notre choix initial est faux” équivaut maintenant à “le cadeau se trouve derrière l’autre porte”, on a deux chances sur trois de gagner si on change de porte…

Pas convaincu ? Alors imaginez le même jeu avec un million de portes.

Vous pensez toujours que c’est une chance sur deux ?

Alors laissez-moi vous demander combien vous serez prêt à donner pour un ticket d’Euromillion gagnant à une chance sur deux ? Comme je suis sympa, je vous le fais à 1000€ seulement.
Voici comment on procédera : j’achète un ticket d’Euromillion. Ensuite je regarde les résultats (et pas vous). Et je vous propose deux combinaisons, la mienne et une autre. Sur ces deux combinaisons, l’une sera gagnante, promis. Donc en m’achetant le ticket, vous aurez une chance sur deux de gagner au rang 1. Et pour mille euros, ça vaut clairement le coup...

La vie est incertaine

Le hasard est partie intégrante de nos vies. Par sa nature même, le futur est incertain. Pourtant nous devons effectuer nos choix présents en fonction de nos prédictions de ce futur. La capacité à prédire l'incertain est donc une qualité essentielle. En la développant, il est possible de transformer nos incertitudes irrationnelles, floues  et angoissantes en incertitudes rationnelles, mesurées et apaisantes.

Dieu ne joue peut être pas aux dés mais nous si, tout le temps. Avant de parier sur un double 6, mieux vaut en connaître sa probabilité...