Comment battre les fishs calling station en No Limit

18 mai 2016
petiteglise
7913
PA 0
7 Commentaires

Après avoir expliqué qu’un mauvais call d’un fish peut, paradoxalement, nous faire perdre de l’Ev, nous allons voir comment vous pouvez en profiter.

Cet article est la suite de Pourquoi vous perdez (trop souvent) contre les fishs calling stations. Vous pouvez lire cet article de manière indépendante mais pour une meilleure compréhension je vous recommande de commencer par le précédent. Dans mon dernier article, j’avais illustré le théorème de Morton, à savoir qu’un mauvais call adverse peut faire diminuer notre Ev, par l’exemple donné par Morton lui même, en Limit Holdem. Nous allons maintenant aborder le cas du No Limit, et voir comment nous pouvons retourner le théorème de Morton à notre avantage.

Le théorème de Morton en No Limit

Le board est
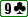
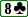
Vous êtes au BTN avec
Fish 1 en SB a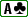
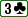
Fish 2 en BB a
Il y a 100€ dans le pot, les blinds checkent, vous misez 39. (La mise est quelque peu étrange mais permet au paradoxe de bien fonctionner)

Fish 1 paie avec ses 9 outs.
Fish 2 doit mettre 39 dans 178 avec 6 outs. S’il fold, il perd 0, s’il call, il perd 178*6/42-39*36/42=-8€ Le call de Fish 2 est donc une erreur.

Si Fish 2 fold, vous avez déjà mis 33.3+39=72.3€ vous jouez pour 178€ contre 9 outs. Votre Ev est de 178*33/42-72.3=67.6€

Si Fish 2 call, vous jouez pour 217€ contre 15 outs 217*27/42-72.3=67.2€
A cause de l’erreur de Fish 2, votre Ev est passée de 67.6 à 67.2€

On est bien dans le cas de la fameuse zone paradoxale du théorème de Morton : vous auriez préféré que Fish 2 fold, même si c’est le meilleur coup pour lui. Autrement dit, vous avez perdu de l’Ev à cause d’un fish calling station…

Comment retourner le théorème de Morton à votre avantage.

Sur le spot vu juste au-dessus, vous auriez souhaité que la BB ne soit pas un fish et se couche. Mais est-ce vrai sur le long terme ?

Pour comprendre ce qui se passe sur le long terme, on peut considérer que vous aurez ce spot 6 fois : 2 fois au bouton, une avec Fish 1 en SB, l’autre avec Fish 2 en SB et de manière similaire, vous aurez ce spot 2 fois en SB et 2 fois en BB.
Analysons ce qui se passe dans chaque cas.

Ev du BTN si les deux fold : 100-33.3=66.6€
Ev du BTN si SB call et BB fold : 178*39/42-72.3=67.6€
Ev du BTN si les deux call : 217*33/42-72.3=67.2€

Ev de la SB si elle fold : -33.3€
Ev de la SB si elle call et BB fold : 178*9/42-72.3=-34.2€
Ev de la SB si elle call et BB call : 217*9/42-72.3=-25.8€

Ev de la BB si elle fold : -33.3€
Ev de la BB si SB a call et elle call : 217*6/42-72.3=-41.4€

Deux remarques :
On peut considérer que le call en SB est une erreur car si la BB fold, elle n’a pas la cote.
On n’envisage pas le cas où SB fold et BB paie.

Pour les deux cas où vous êtes au bouton, les deux fishs vont payer, vous aller gagner 67.2*2=134.4
Pour les deux cas où vous êtes en SB, vous allez vous coucher et perdre 33.3*2=66.6
Pour les deux cas où vous êtes en BB, vous allez vous coucher et perdre 33.3*2=66.6

Au total, vous aurez gagné 134.4-66.6*2= 1.2€ Fish 1 et Fish 2 ont perdu la même chose et à eux deux ils ont perdu ce que vous avez gagné, soit -0.6€ chacun.

Youhou ! 6 mains contre des fishs, vous ne faites pas d’erreur, vous êtes récompensé en gagnant 1.2€ ! Enfin ça c’est sans compter le rake, en réalité vous ne seriez même pas break-even…

En fait, vous avez joué parfaitement au sens GTO du terme, mais avez commis une erreur d’un point de vue exploitant. En SB, sachant que BB va commettre l’erreur de payer, vous devez payer et non vous coucher.
Dans ce cas, votre Ev totale est de 67.2*2-25.8*2-33.3*2=16.2
Vous gagnez 16.2€ sur les 6 mains et chaque fish perd donc 8.1€.

Vaut-il réellement mieux affronter un seul fish que deux ?

Dans le premier exemple, vous auriez préféré que la BB ne soit pas un fish et se couche. Mais que se passe-t-il à long terme si vous affrontez un seul fish ?

Quand le fish est à votre gauche, vous rasez :
Au BTN, il paie en SB, la BB fold, vous prenez 67.6
En SB, vous payez sachant qu’il va payer en BB, vous perdez 25.8
En BB, vous vous couchez et perdez 33.3
Au total, vous gagnez 8.5€

Quand le shark est à votre gauche, c’est bien moins glorieux.
Au bouton, le shark paie en SB sachant que le fish va payer, vous prenez 67.2
En SB, vous vous couchez en sachant que le shark va se coucher et perdez 33.3
En BB, vous vous couchez et perdez 33.3
Au total, vous gagnez 0.6€

En additionnant les deux sous-totaux, vous arrivez à 9.1€ en 6 mains. Soit beaucoup plus que lorsque vous jouez GTO contre deux fishs, mais beaucoup moins que lorsque vous jouez exploitant contre deux fishs. L’autre shark aura lui aussi gagné 9.1€ Et le fish aura donc perdu 18.2€, soit plus que lorsqu’un deuxième fish était présent.

Le paradoxe a perdu son mystère et on peut conclure qu’il vaut simplement mieux oublier la GTO en micro-limites.