Bonjour à tous,
Je suis actuellement en train d’étudier le livre “Applications of no-limit hold’em” de Matthew Janda et je bloque au chapitre 11 “river play” dans la sous partie pinpointing the optimal river bet size. C’est pourquoi je me tourne vers vous pour avoir quelques explications à ce sujet.
Ce qui me pose problème est l’application de la formule suivante qui nous permettrait de déterminer la taille de notre bet afin d’atteindre la plus haute EV
0 = 1 - (2Y)(1 + 2X + X^2)
où X est la taille de notre bet en pot size bet et
Y la fréquence à laquelle nous perdons
après avoir tenté de réaliser quelques exemples moi même j’ai l’impression de mal appliquer cette formule, pourriez-vous m’indiquer comment l’utilisez-vous (ou l’utiliseriez-vous) et me faire part du quadratic solver que vous utilisez ?
Pour ceux qui sont familiers avec le bouquin, pourriez-vous utiliser d’autres exemples que ceux indiqués dans ce chapitre ?
Merci
déjà isole le betsize :
X = -(2*Y+sqrt(2)*sqrt(Y))/(2*Y)
ou
X = (sqrt(2)*sqrt(Y)-2*Y)/(2*Y)
Ensuite, pour une main donnée tu fais un postulat sur la range de vilain (genre il call/win 25% du temps et il raise 10% du temps, ce qui donne 35% du temps où tu perds. Du coup tu mets 0.35 à la place de Y, ce qui donne ici un bet optimal de 20%~ du pot.
disclaimer : je fais les calculs en fonction de ton message, j’ai pas le livre en question. Je suis d’ailleurs un poil surpris qu’on ait pas en variable le % call/fold ou la FE…
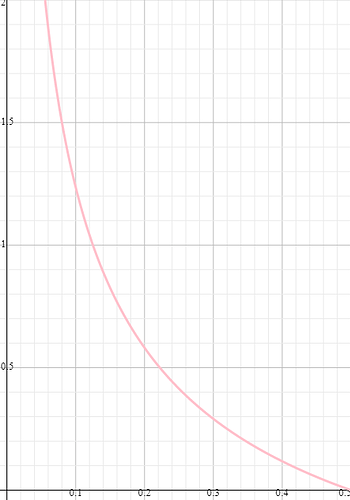
Merci beaucoup pour la réponse et sa pertinence. Cela correspond exactement à ce que je cherchais, Voici un graphique de la deuxième équation proposée du bet size (en pot size bet) en fonction du temps où nous perdons effectivement.
En pratique, cela donne quoi sur ton exemple ? On observe rarement un sizing à 20% (et je pense que j’ai toujours perdu contre ce genre de sizing). Maintenant, à la rivière en petites limites, est souvent uniquement en value. Ton hypothèse n’est peut être pas réaliste
Cette manière de déterminer un sinzing optimal river n’est effectivement pas valable dans de nombreuses situations (et peut-être même aucunes). J’ai quand même trouvé l’approche intéressante. Je vais tâcher de l’expliquer :
Le but étant de comprendre notre erreur si l’on bet trop cher ou trop petit. Si l’on bet trop cela implique que l’on perd plus d’argent face aux mains qui nous battent et va faire fold notre adversaire plus de mains que l’on bat. Si l’on bet trop petit cela implique que l’on obtient trop peu de value des mains que l’on bat.
Comme Y représente la fréquence à laquelle nous perdons effectivement la formule est capable de prendre en compte la capacité de notre adversaire à raise en bluff. Et comme le livre est basé sur un jeu qui serait GTO cela implique que si notre adversaire nous bluff avec une range balancée on a effectivement perdu la main.
Ensuite Y changera en fonction de la taille de notre bet, des profondeurs et du removal effect.
Si on prend l’exemple où vilain nous bat 40% du temps la formule nous donne un résultat de 0.12PSB. Effectivement nous n’allons pas bet à chaque fois 0.12PSB parce que nous avons trouvé ce résultat avec cette démarche. Cela pourrait être intéressant face à un adversaire qui ne pourrait que défendre par un call mais il faut être prudent quand un check raise est possible. Cette formule ne va pas nous dire s’il est plus profitable de check ou de bet en position car bet ré-ouvre l’action et permet à vilain de raise.
Les petits bets font sens théoriquement OOP car ils ne ré-ouvrent pas le bet.
Quand les stacks sont plus petits et que faire all in est une option la formule ne fonctionnera pas car vilain ne peut pas raise après notre mise all in et qu’en allant all in pour un petit montant on l’oblige à call avec une range large. En effet, il est quelquefois correct de partir à tapis OOP quand nous sommes battus plus de la moitié du temps face à la range de vilain.
1 « J'aime »
Le fait que vilain puisse réouvrir l’action en te raisant ne changent vraiment pas grand chose, dans la mesure, ou si il est balanced, tu vas être obligé de call une partie du temps, et donc capturer une partie du pot. En gros, quand il raise, t’as le droit de bluffcatch, t’as pas tout le temps perdu.